Most Recent in ArcGIS Blog
Crafting conservation stories — protecting our planet, one story at a time
Get storytelling advice and conservation inspiration from the winners of the 2023 ArcGIS StoryMaps Competition.
Identify the best location for an urgent care center
Multiple Authors | Analytics | April 2, 2024
Use suitability analysis in ArcGIS Business Analyst Web App to locate a site for a new urgent care center in Maverick County, Texas.
Most Recent in ArcGIS Blog
Multiple Authors | ArcGIS StoryMaps | Apr 22, 2024
Get storytelling advice and conservation inspiration from the winners of the 2023 ArcGIS StoryMaps Competition.

Greg Lehner | ArcGIS Pro | April 22, 2024
If you receive a notification saying there's a drawing alert: don't panic! Let's solve it together.

Kerri Rasmussen | ArcGIS Field Maps | April 22, 2024
Start using Arcade in the Field Maps Designer.

Multiple Authors | ArcGIS Enterprise | April 22, 2024
Representing the user experience during Utility Network design, Mohan Punnam details the importance of keeping users at the forefront.
Multiple Authors | ArcGIS Living Atlas | April 19, 2024
Esri joins Overture Maps Foundation, supporting its mission to create reliable, easy-to-use, and interoperable map data for the globe.
Multiple Authors | ArcGIS Hub | April 18, 2024
Shawnlei Breeding shares her strategies for engaging volunteers and stakeholders to help protect eagles across The State of Florida.

Shane Matthews | ArcGIS Online | April 18, 2024
Esri's Basemaps continue to improve with over 300 new and updated communities, spanning 4 continents.

Multiple Authors | ArcGIS Hub | April 17, 2024
Hubs provide a virtual place for collaboration and engagement to happen within communities of all types and sizes.

Owen Evans | ArcGIS StoryMaps | April 17, 2024
Image gallery has made its way to briefings, and you can highlight a feature in a map by showing its pop-up.
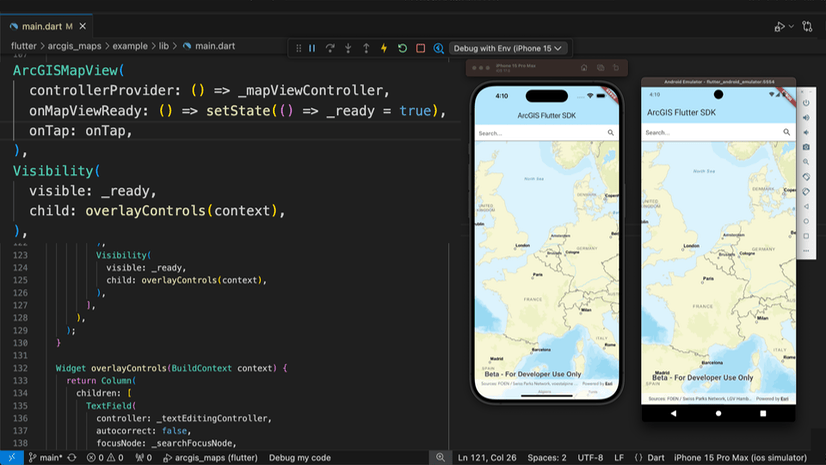
Multiple Authors | Developers | April 17, 2024
We are excited to announce the new ArcGIS Maps SDK for Flutter beta is now available!
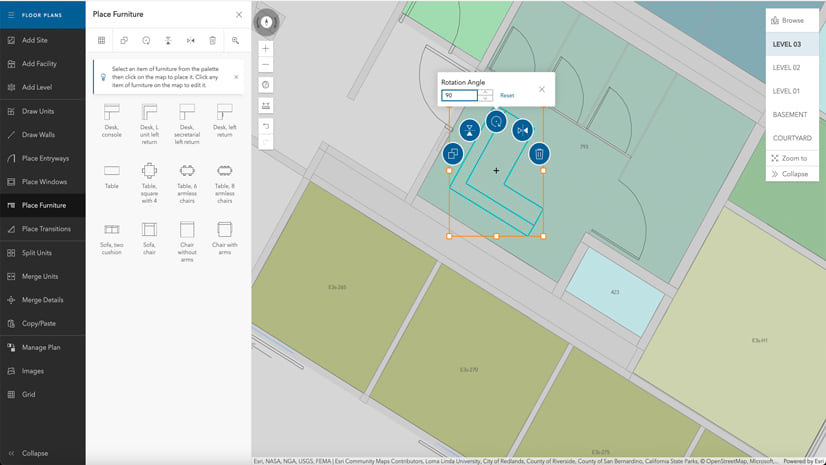
Multiple Authors | ArcGIS Indoors | April 17, 2024
Explore questions and answers from our webinar about Indoor GIS: Easy indoor map creation

Jeff Liedtke | ArcGIS Pro | April 16, 2024
Format your metadata for the video multiplexer tool to geoenable video data for the Full Motion Video player.

Multiple Authors | ArcGIS Enterprise | April 15, 2024
From emergency management to utilities, journey with Mark Sanders of Entergy, as he shares his passion for GIS.

Emily Garding | ArcGIS Online | April 12, 2024
Get more precision while editing in ArcGIS Online using interactive tooltips to set your own editing constraints.

John Nelson | ArcGIS Pro | April 12, 2024
How to configure scale-appropriate contour lines and their labels.
Bern Szukalski | ArcGIS Online | April 11, 2024
By default the ArcGIS World Geocoding Service is the locator used across your organization. Here's how to configure and use a locator view.
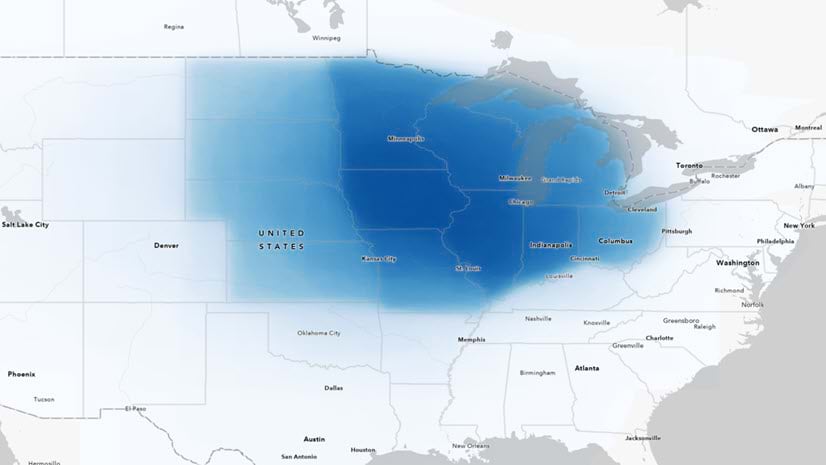
Multiple Authors | ArcGIS Survey123 | April 11, 2024
Answering regional geographers' favorite question: Where is the Midwest to you?
Rajinder Nagi | ArcGIS Living Atlas | April 11, 2024
In April 2024, elevation layers have been updated with high-res datasets of Wales, New Zealand & German states of Bavaria, Saxony and Brandenburg

Multiple Authors | Developers | April 11, 2024
Version 200.4 of the ArcGIS Maps SDKs for Native Apps includes support for feature forms, snapping, OGC 3D Tiles, and more!

Multiple Authors | ArcGIS Maps SDK for Unreal Engine | April 11, 2024
ArcGIS Maps SDK 1.5 for Unreal Engine adds support for Esri's global OSM 3D Buildings layer, group layers, and more!

Multiple Authors | ArcGIS Maps SDK for Unity | April 11, 2024
ArcGIS Maps SDK 1.5 for Unity adds support for Esri's global OSM 3D Buildings layer, group layers, and more!
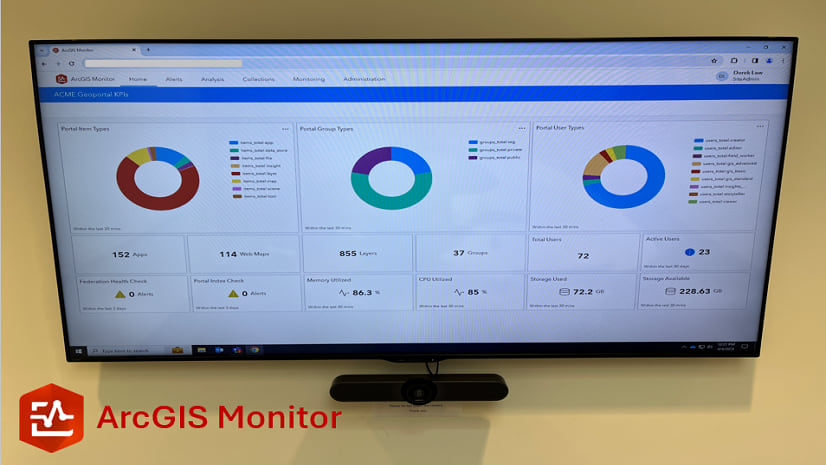
Multiple Authors | ArcGIS Monitor | April 10, 2024
This blog presents six useful indicators that provide insight on Enterprise portal performance metrics.

Multiple Authors | ArcGIS Pro | April 10, 2024
With ArcGIS Pro 3.2 or later, you can export all symbols in your project to a custom style.

Raluca Nicola | ArcGIS Maps SDK for JavaScript | April 10, 2024
A small hack for adding a watercolor basemap to a 3D city visualization

Mindy Longoni | ArcGIS Solutions | April 10, 2024
Maintain a road-closure inventory and share important road information with the public with the Road Closures solution.

Stephanie Umeh | ArcGIS Experience Builder | April 9, 2024
This blog article showcases an inventory of GIS-related web applications and maps built in 2023 using ArcGIS Experience Builder.
