By Dr. A Jon Kimerling, Professor Emeritus, Oregon State University
There are many ways that we can think about similarities among map projections. We can group projections as similar in map scale or as serving similar user communities. Cartographers often take a different approach and group projections by similar geometrical properties or by similar mathematics underlying their construction. Grouping projections into cylindrical, conic, and azimuthal classes is an example of grouping by similar geometrical properties, whereas categorizing projections as conformal, equal area, and equidistant is an example of grouping by similar distortion properties that are a consequence of the mathematics underlying the projections.
In this blog I would like to introduce another way of thinking about similarities among projections — that seemingly distinct projections may actually be parts of a continuum of projections created by varying the parameters of a single pair of projection equations transforming latitude and longitude coordinates on the sphere or ellipsoid into (x,y) Cartesian coordinates on the flat projection surface. Such projection continuums are best illustrated by animations that show the changes in the graticule and coastline as a certain projection parameter is varied systematically through a large range of values. I hope you will find these animations useful in your quest for further understanding the nature of map projections.
Mercator Aspects Continuum
You undoubtedly learned in your beginning cartography class or textbook that the Mercator Cylindrical Conformal map projection has three basic aspects – normal with the line of tangency along the equator, transverse with the line of tangency along a meridian and its antipodal meridian, and oblique with the line of tangency being any other great circle on the sphere. More advanced books give the different sets of map projection equations that are used for each of these aspects. You may have noticed, however, that the normal and transverse aspects are actually endpoints of the oblique aspect Mercator projection equations, and that a continuum of oblique aspect projections must exist between these endpoints.
You can make an animation showing this continuum in ArcMap by transforming the graticule and coastlines using the Hotine Oblique Mercator Azimuth Center projection which is in the Projected Coordinate Systems for the World on the Modify tab for the Mercator world projection. I created the animation titled “Mercator Aspects Continuum” from ninety Hotine Oblique Mercator projections, each centered at (0°, 0°) and ranging in azimuth angle from 0° to 90° in one degree increments. Changing the azimuth angle by one degree increments from 0° shifts the line of tangency from the equator to a great circle with maximum and minimum latitudes of 1°N and 1°S, 2°N and 2°S, and so on until the limit of 90°N and 90°S is reached for the meridians forming the line of tangency for the transverse aspect.
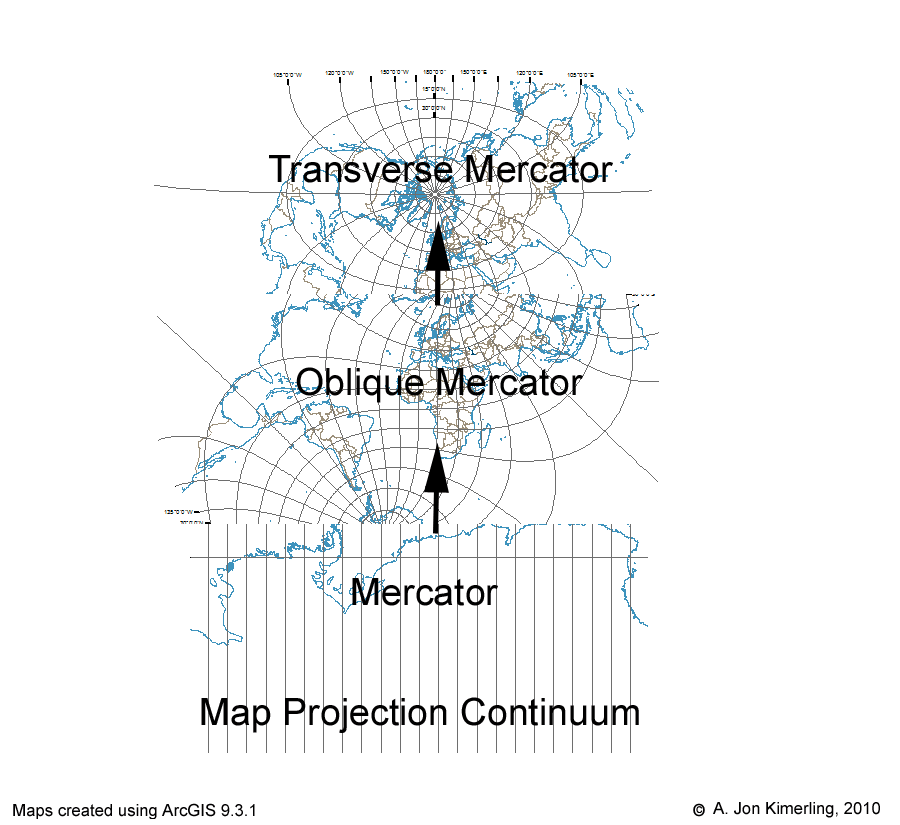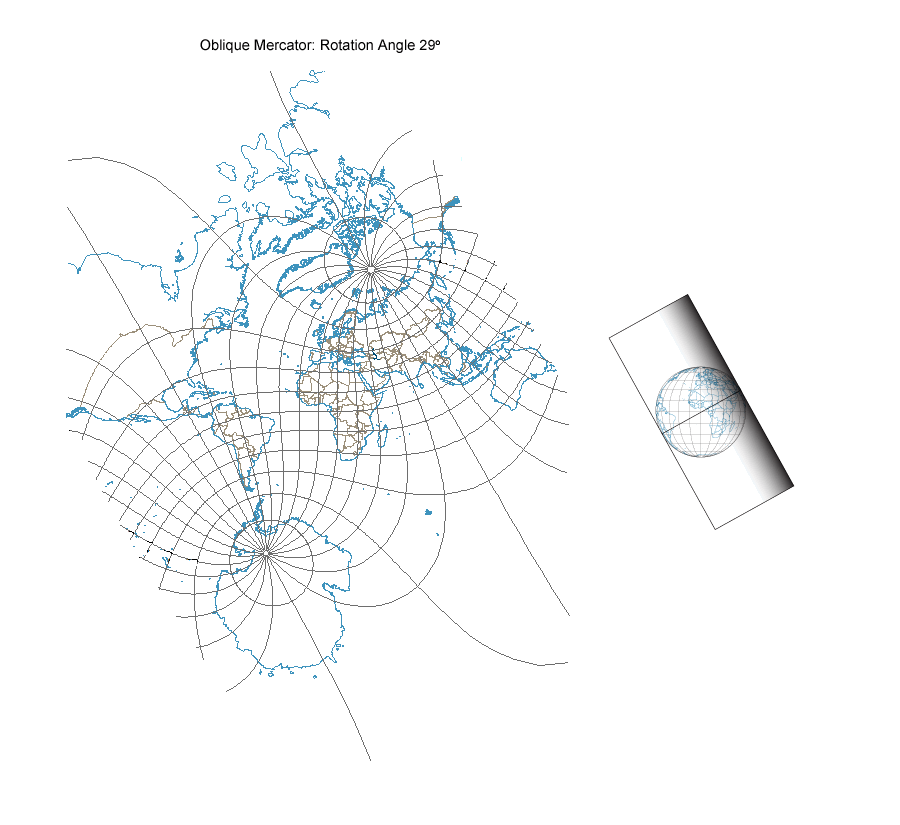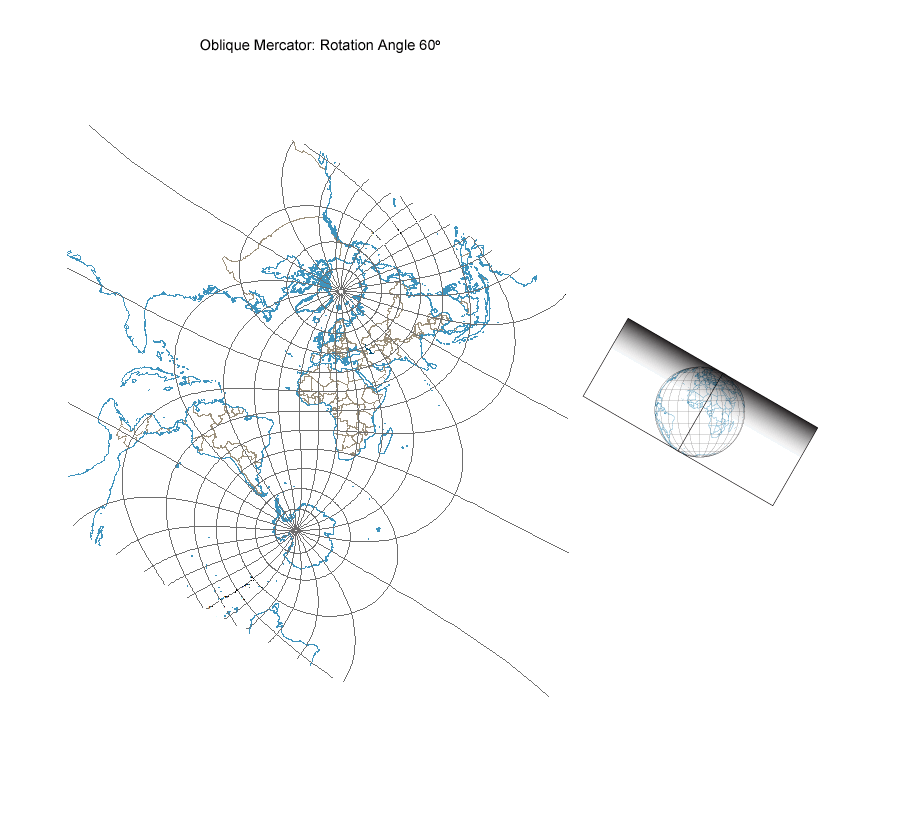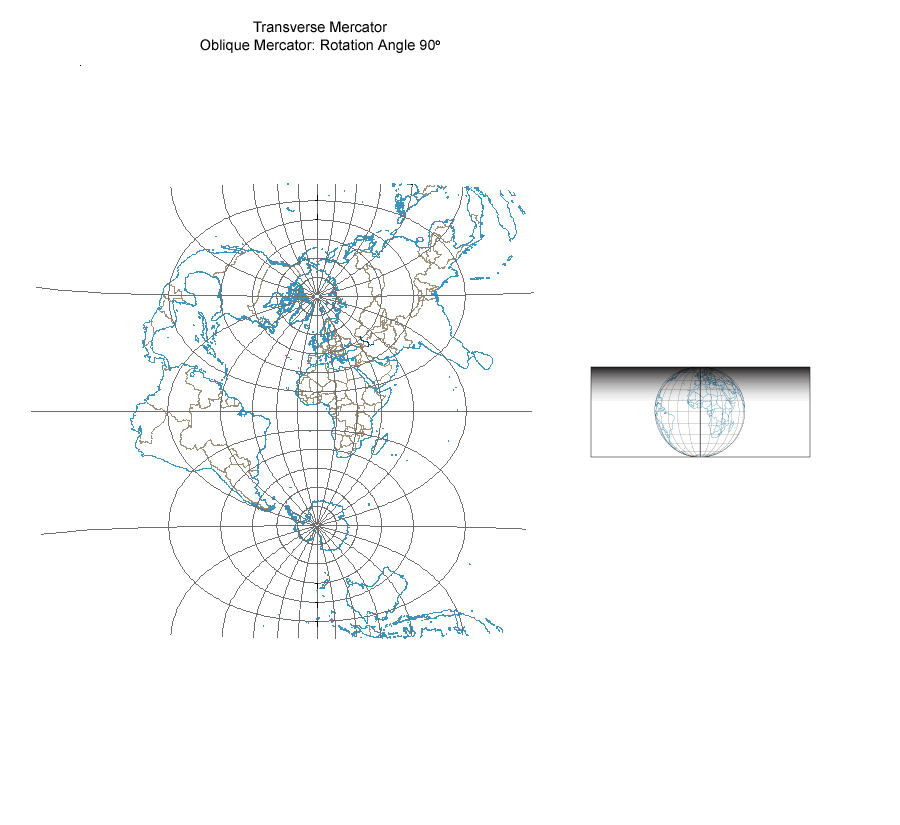
The Mercator Aspects Continuum.
To further illustrate the geometrical nature of the Mercator aspect continuum, I used Adobe Illustrator to create a cylinder that I could place at different azimuth angles on an equatorial aspect Orthographic projection of the hemisphere from 90°W to 90°E. The straight line bisecting the projection is the line of tangency for the projection at the particular azimuth angle. Be aware that the Hotine Oblique Mercator (as well as the normal and transverse aspect Mercator) projection is not a true perspective projection that could be created optically by projecting a point light source in the middle of a transparent globe to the surface of the cylinder. Rather, all three Mercator aspects are created from moderately complex mathematical equations that give a conformal surface on the cylinder. The rotating cylinder and line of tangency should help you understand the radical changes in the appearance of the graticule and coastline that you see along the continuum from the normal to transverse Mercator aspects.
True-perspective Azimuthal Projection Continuum
In addition to the three aspects of the Mercator projection, you probably studied azimuthal map projections including the gnomonic, stereographic, and orthographic. The gnomonic and orthographic projections are actually endpoints of the far-side true perspective projection continuum that I show in the animation titled “Azimuthal Continuum”. The projections that form this animation were created through a C language program that I wrote in which each north polar aspect projection was created from the oblique triangle trigonometry equations shown in the illustration below (an example of projecting at the 45°N parallel).
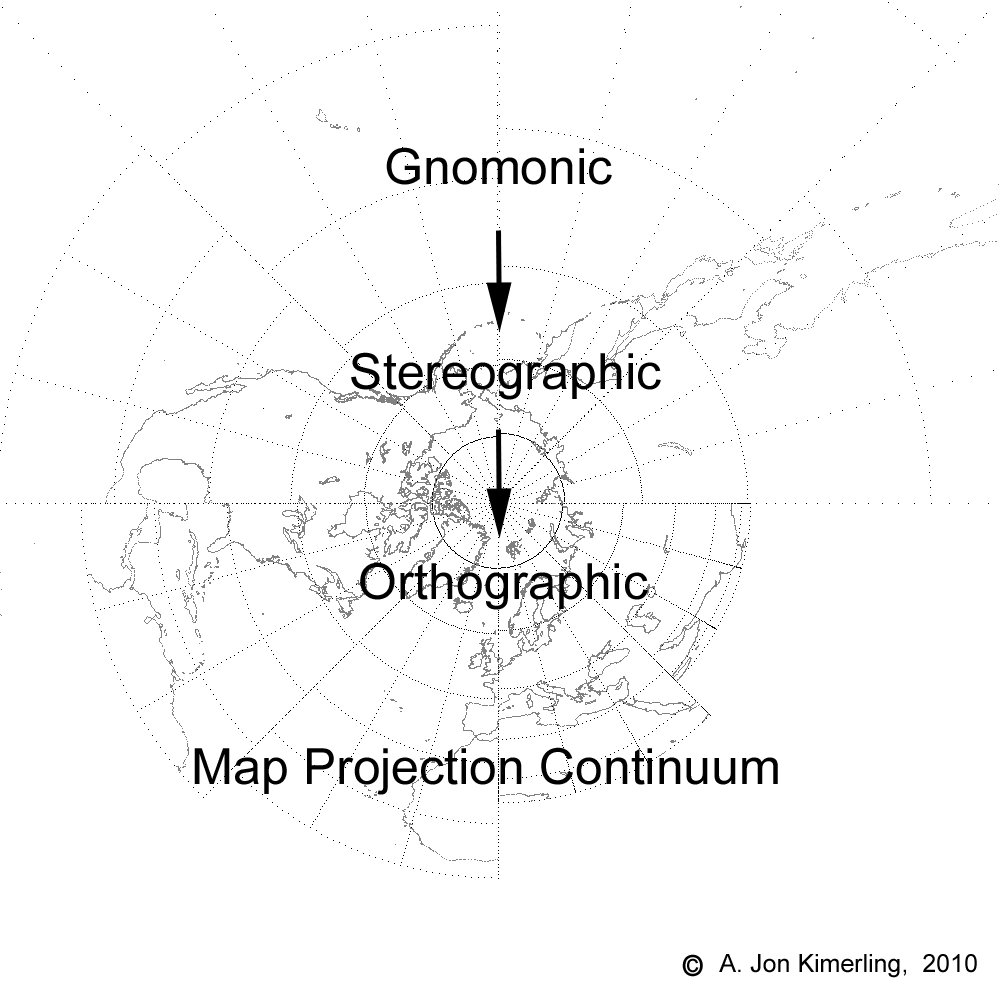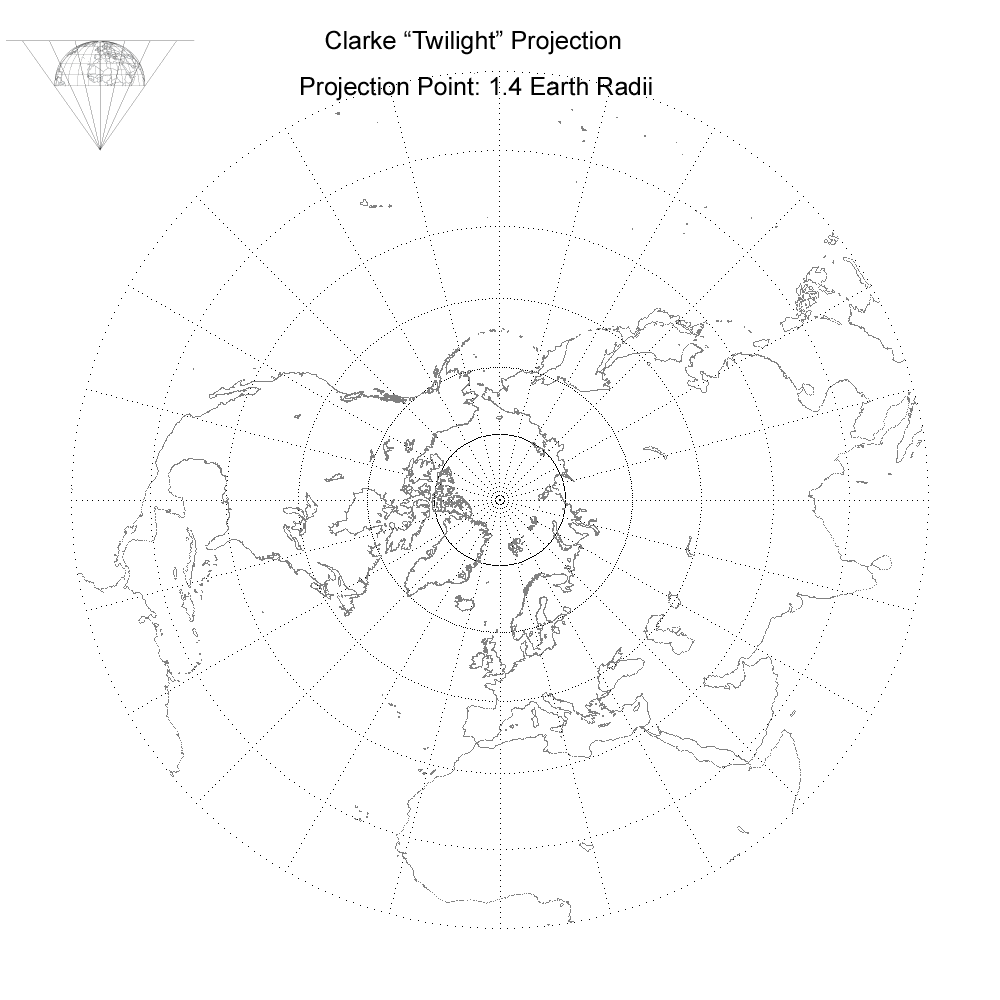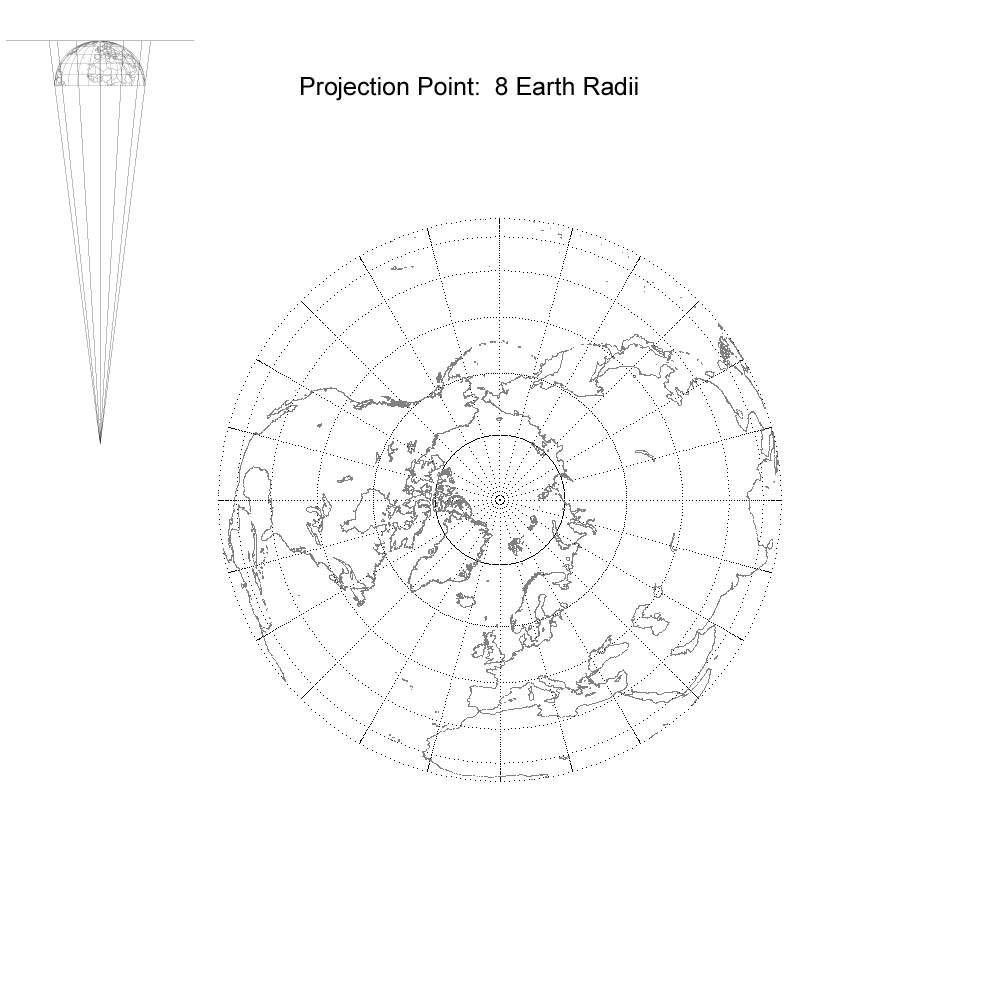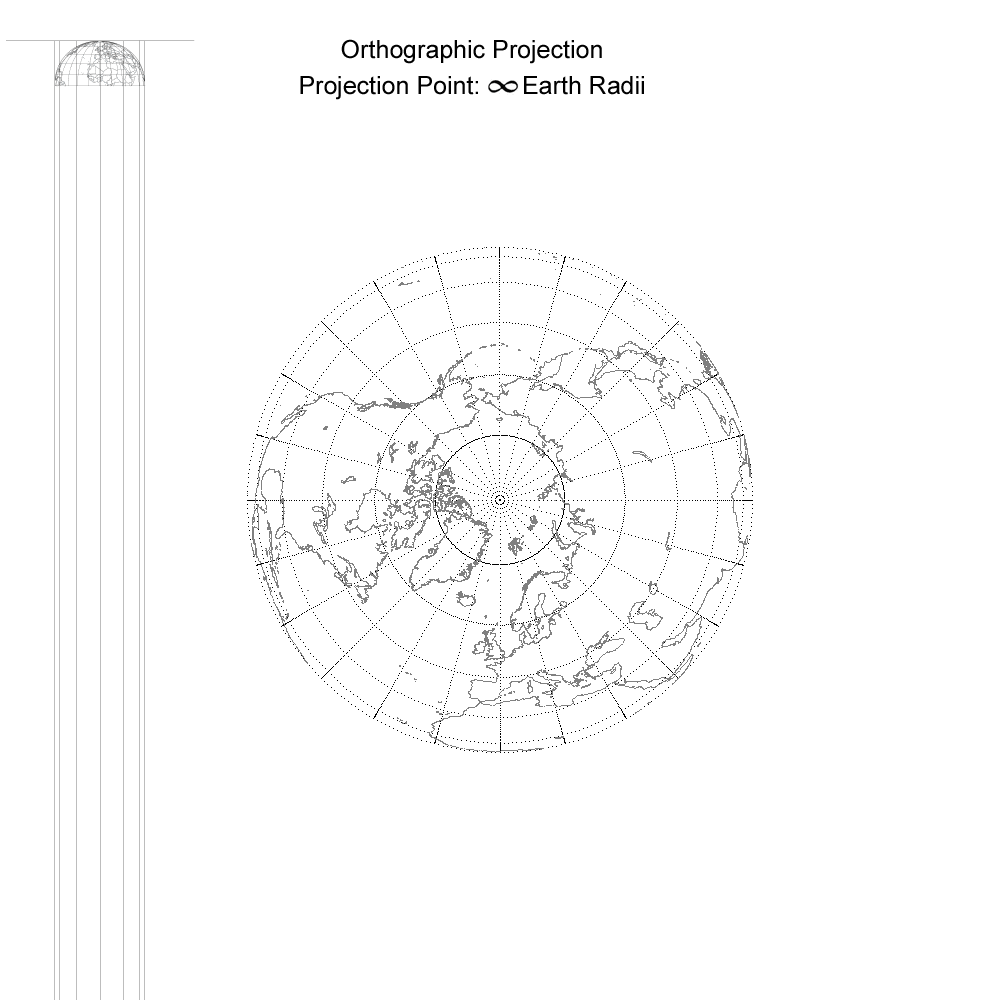
The Azimuthal Continuum.
Notice that for the gnomonic projection with the projection point at the earth’s center the distance from the center is 0.0, so that b = 1, ? = ?, and p = tan (?). For the stereographic projection d = 1 , ? = 0.5 ?gnomonic, and p = 2.0 tan(0.5 ?gnomonic). The orthographic projection with the projection point an infinite distance is interesting mathematically. It turns out that as d approaches infinity and ? concurrently approaches 0 degrees, the two limits converge to values of p defined by the equation p = cos(latitude).
Notice that three additional true perspective projections developed in past centuries have been identified along the continuum at different projection point distances– the Clarke “twilight” (1.4 radii), James polar (1.5 radii) and LaHire polar (1.71 radii). The diagrams on the left edge of each map in the animation illustrate correctly the projection point distance and rays from the projection point through the equator, 30°N and 60°N parallels. Unfortunately, the length of rays for projection points greater than 25 earth radii were too long to fit vertically on the page and hence had to be clipped at the bottom.
Mercator – Lambert Conformal Conic – Polar Stereographic Continuum
In 1772, Johann Heinrich Lambert published in German his landmark Notes and Comments on the Composition of Terrestrial and Celestial Maps which was translated into English in 1972 by Waldo Tobler. In discussing the derivation of the projection we now know as the Lambert Conformal Conic projection, Lambert noted that: “Stereographic representations of the spherical surface, as well as Mercator’s nautical charts, have the peculiarity that all angles maintain the sizes that they have on the surface of the globe. This yields the greatest similarity that any plane figure can have with one drawn on the surface of a sphere. The question has not been asked whether this property occurs only in the two methods of representation mentioned or whether these two representations, so different in appearances, can be made to approach each other through intermediate stages.” The Lambert Conformal Conic projection is the intermediate projection that answered this question in the affirmative. Indeed, John Snyder notes in his Map Projections – A Working Manual (1987) that if the standard parallels for the Lambert Conformal Conic projection are symmetrical about the equator, the regular [normal aspect] Mercator projection results. At the other extreme, if the only standard parallel is at a pole, the polar Stereographic projection results. The Lambert Conformal Conic projection is normally constructed as a secant case projection with two standard parallels, but it also can be created as a tangent case projection with a single standard parallel (or by making the two standard parallels identical, as I did in ArcMap). I was thus able to create a continuum of ninety Lambert Conformal Conic projections beginning with the standard parallel at the equator for the regular Mercator projection, and then increasing in increments of one degree to the pole where the north polar Stereographic projection resulted. The animation I created from these ninety projections is titled “Mercator Lambert Stereographic Continuum”.

The Mercator Lambert Stereographic Continuum.
To further illustrate the geometrical nature of the Lambert Conformal Conic standard parallel continuum, I used Adobe Illustrator to create a series of cones of different heights that I could place at different standard parallels on an equatorial aspect Orthographic projection of the hemisphere from 90°W to 90°E. Be aware that the Lambert Conformal Conic projection is not a true perspective projection that could be created optically by projecting a point light source in the middle of a transparent globe to the surface of the cone. Rather, the ninety Lambert Conformal Conic projections are created from moderately complex mathematical equations derived by Lambert that give a conformal surface on the cone. The shape of the cone and position of the line of tangency should help you understand the radical changes in the appearance of the graticule and coastline that you see along the Lambert Conformal Conic continuum with the Mercator and Stereographic as endpoint projections.
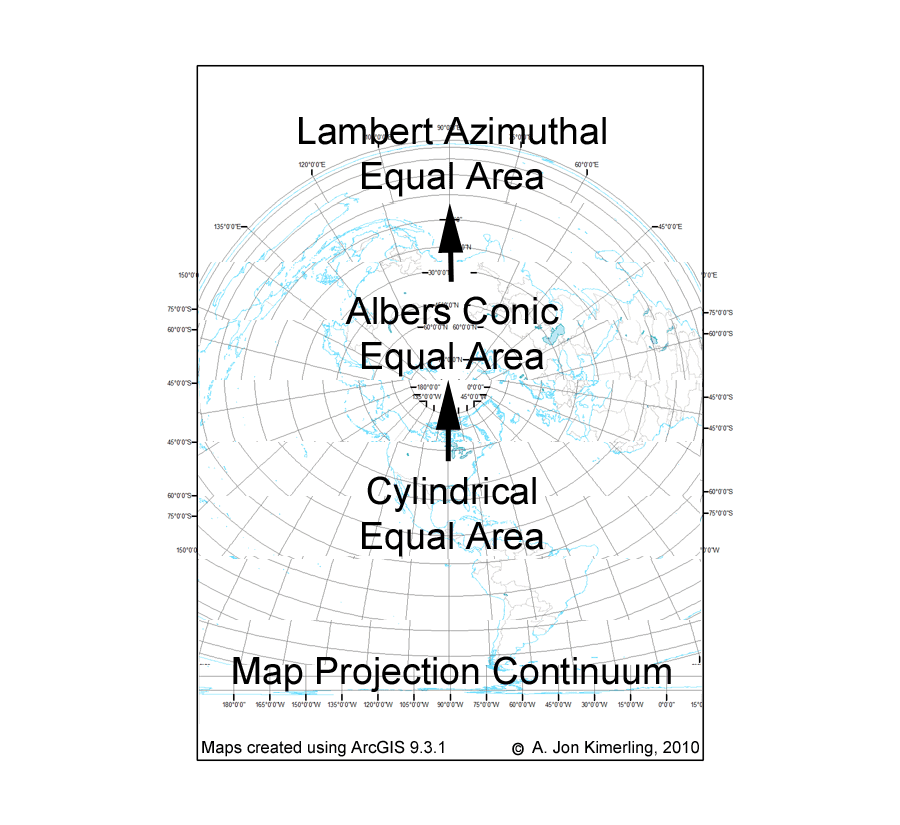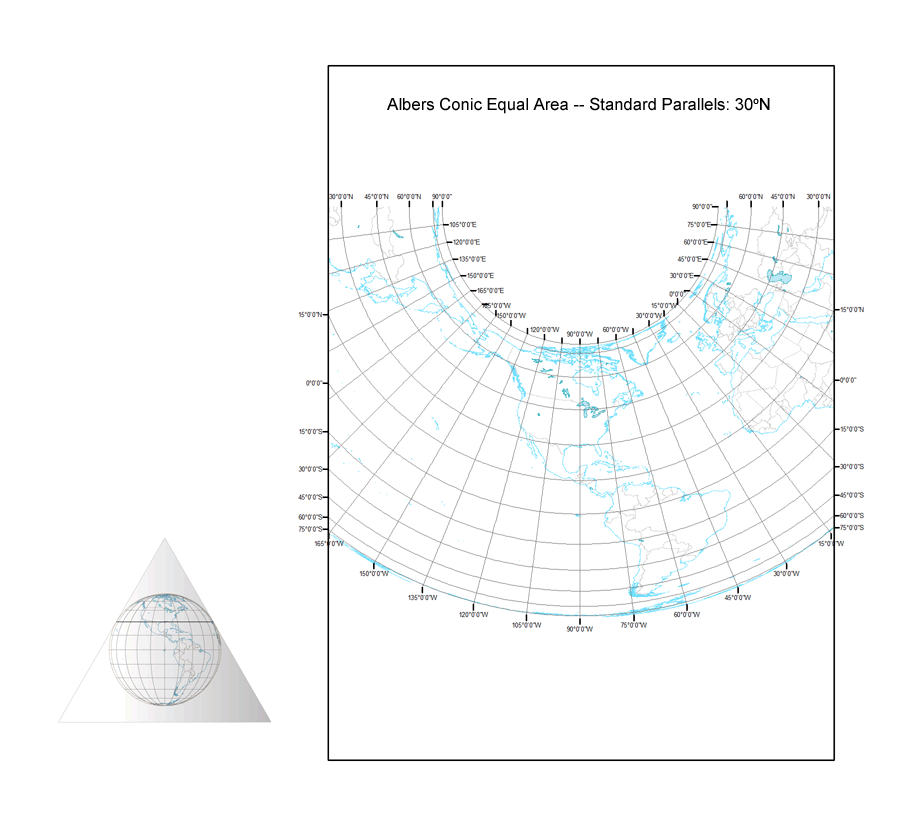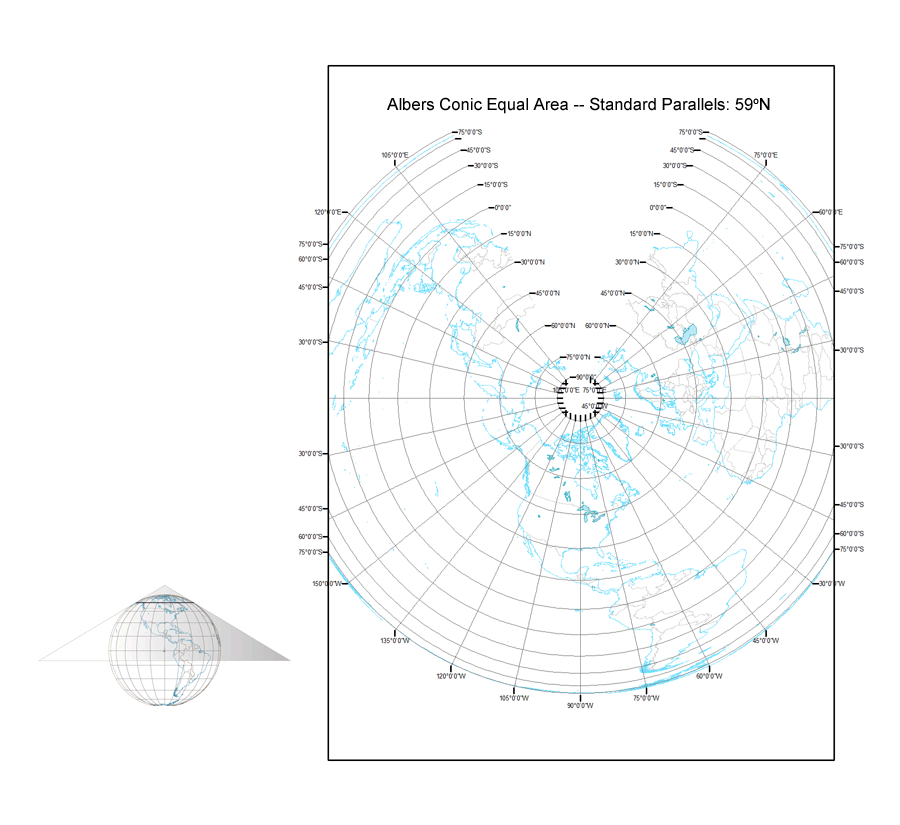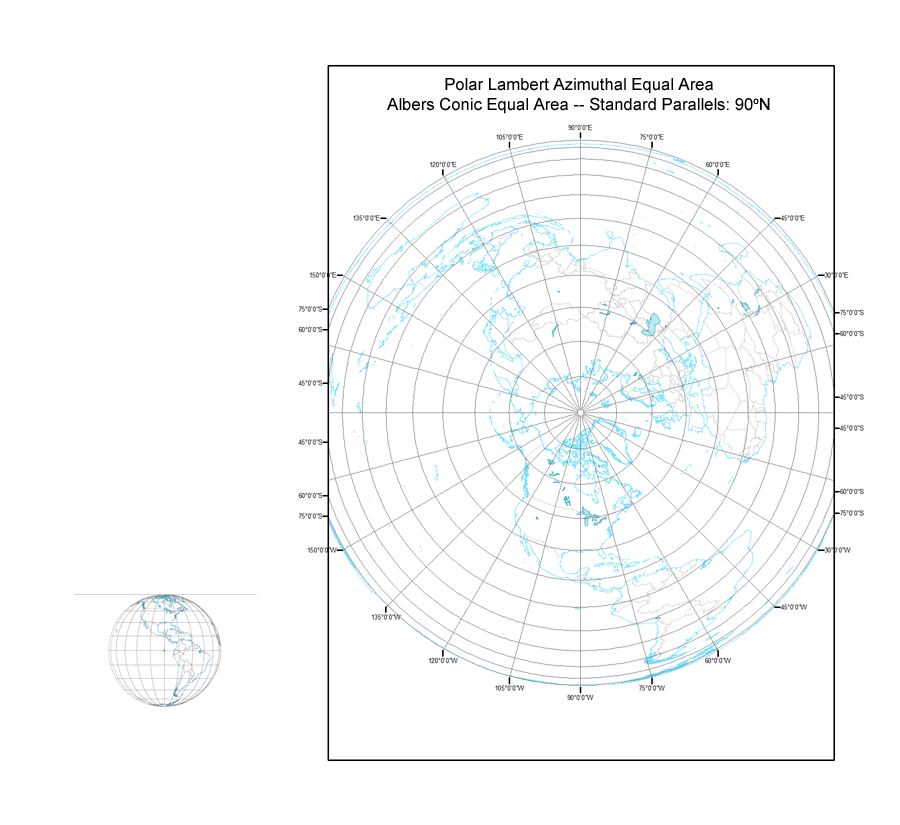
Lambert Cylindrical Equal Area – Albers Equal Area Conic – Polar Lambert Azimuthal Equal Area Continuum
John Snyder notes in his Map Projections – A Working Manual (1987) that if the equator is the standard parallel for the Albers Equal Area Conic projection, the projection becomes the Lambert Cylindrical Equal Area projection. The Albers Equal Area Conic projection is normally constructed as a secant case projection with two standard parallels, but it also can be created as a tangent case projection with a single standard parallel (or by making the two standard parallels identical, as I did in ArcMap). Setting the pole as the standard parallel creates the polar aspect of the Lambert Azimuthal Equal Area projection. Hence, the two Lambert projections are endpoints for a continuum of Albers projections with one standard parallel ranging from 0 to 90 degrees. The animation I created from these ninety projections is titled “Albers Continuum”.

The Albers Continuum.
As with the Lambert Conformal Conic projection continuum, I used Adobe Illustrator to create a series of cones of different heights that I could place at different standard parallels on an equatorial aspect Orthographic projection of the hemisphere from 90°W to 90°E. Be aware again that the Albers Equal Area Conic projection is not a true perspective projection that could be created optically by projecting a point light source in the middle of a transparent globe to the surface of the cone. Rather, the ninety Albers projections are created from moderately complex mathematical equations derived by Heinrich Albers in 1805 that give an equal area surface on the cone. The shape of the cone and position of the line of tangency should help you understand the radical changes in the appearance of the graticule and coastline that you see along the Albers Equal Area Conic continuum.
Plate Carrée – Equidistant Conic – Polar Azimuthal Equidistant Continuum
John Snyder notes in his Map Projections – A Working Manual (1987) that if the equator is the standard parallel for the Equidistant Conic projection, the projection becomes the Plate Carrée projection (also known as the Equidistant Cylindrical projection). He also mentions that setting the pole as the standard parallel creates the polar aspect of the Azimuthal Equidistant projection. The Equidistant Conic projection is normally constructed as a secant case projection with two standard parallels, but it also can be created as a tangent case projection with a single standard parallel (or by making the two standard parallels identical, as I did in ArcMap). Hence, the Plate Carrée and Azimuthal Equidistant projections are endpoints for a continuum of Equidistant Conic projections with one standard parallel ranging from 0 to 90 degrees. The animation I created from these ninety projections is titled “Equidistant Conic Continuum”.

The Equidistant Conic Continuum.
As with the Lambert Conformal Conic and Albers Equal Area Conic projection continuums, I used Adobe Illustrator to create a series of cones of different heights that I could place at different standard parallels on an equatorial aspect Orthographic projection of the hemisphere from 90°W to 90°E. Once more be aware that the Equidistant Conic is not a true perspective projection that could be created optically by projecting a point light source in the middle of a transparent globe to the surface of the cone. Rather, the ninety Equidistant Conic projections are created from moderately complex mathematical equations that give an equidistant surface on the cone. The shape of the cone and position of the line of tangency should help you understand the radical changes in the appearance of the graticule and coastline that you see along the Equidistant Conic continuum.
Sinusoidal – Bonne Conic – Werner Continuum
John Snyder notes in his Map Projections – A Working Manual (1987) that if the equator is the standard parallel for the Bonne Conic equal area projection, the projection becomes the Sinusoidal equal area. He also mentions that setting the pole as the standard parallel creates the Werner projection (also called the Cordiform projection due to its Valentine heart shape). Hence, the Sinusoidal and Werner projections are endpoints for a continuum of Bonne Conic projections with standard parallels ranging from 0 to 90 degrees. The animation I created from these ninety projections created in ArcMap is titled “Bonne Conic Continuum”. I am indebted to Waldo Tobler for suggesting this continuum to me.

The Bonne Conic Continuum.
Albers Standard Parallel Variation Continuum
Another type of map projection continuum is created when we systematically increase or decrease the spacing of standard parallels on secant case projections. I selected the Albers equal area conic projection and used ArcMap to create 45 projections, beginning with standard parallels at the equator and North Pole and ending with both standard parallels placed at 45°N. These 45 projections were combined into the animation titled “Albers Standard Parallel Variations”.
I used Adobe Illustrator to create a series of secant plane lines placed on an equatorial aspect Orthographic projection of the hemisphere from 90°W to 90°E. Once more be aware that the Albers Equal Area Conic is not a true perspective projection that could be created optically by projecting a point light source in the middle of a transparent globe to the surface of the cone. The position of the secant plane line cutting into the globe should help you understand the changes in the appearance of the graticule and coastline that you see along the standard parallel variation continuum.

The Albers Standard Parallel Variations.
Article Discussion: